70以上 n(n-1)/2 formula name 105895-N(n+1)/2 formula name

Recursively, we also know that T(n)=T(n1)n Manipulating this formula a bit, we can see that T(n1)=T(n)n We can then substitute this value into our first equation to see that T(n)nT(n)=n2 Combining some like terms, we see that 2T(n)n=n2 Again, using some algebraic manipulation, we could arrive at T(n)=n(n1)/2, where T(n) is equal to the sum of the first n natural numbers Our notation and the second introduces you to the Sigma notation which makes the proof more precise A visual proof that 123n = n (n1)/2 We can visualize the sum 123n as a triangle of dots Numbers which have such a pattern of dots are called Triangle (or triangular) numbers, written T (n), the sum of the integers from 1 to nUsw auch wenn etwas gekürzt wird in einer Rechenaufgabe verstehe ich nie warum und wieso, vor allem wie zb (n4)!

Arithmetic Progression Wikipedia

N(n+1)/2 formula name

N(n+1)/2 formula name-View Test Prep 4 from ACTUARIAL 1 at Cairo University PMP Formulas Name (Abbreviation) No of Communication Channels Formula n (n1)/2 nThe list is quite long, if the 7 people

How To Prove 1 2 3 N Terms N N 1 2 Quora

Plugging 4 into the equation we get 4 (41)/2 = 12/2 = 6 So there are 6 possible combinations with 4 items Applying the intuitive understanding of division as repeated subtraction, we can plot 12 on a numberline, and then since we are dividing by 2, we count backwards by 2 until we reach 0 We can do this 6 times That makes sense to meI also know (1) n * n is the formula to find the n th term I just don't understand how the formula n/2 (n % 2 * n) adds all the terms and outputs the same result as ifGet the list of basic algebra formulas in Maths at BYJU'S Stay tuned with BYJU'S to get all the important formulas in various chapters like trigonometry, probability and so on

The formula is simply n!X = N (N1) (N2) 3 2 1 Now, we add up the two expressions, by combining terms is the same position; ((n2)!)/((n1)!) = ((n2)(n1)(n)(n1)(n2) 1)/((n1)(n2)1) ((n2)!)/((n1)!) = (n2)(n1)(n)

Download Page POWERED BY THE WOLFRAM LANGUAGE Standard computation time exceeded Try again with Pro computation time Related Queries fib(T a x) fib(D a y) plot (n^2 n 1)/(n^4 n^2) series (n^2 n 1)/(n^4 n^2) (integrate (n^2 n 1)/(n^4 n^2) from n = 1 to xi) (sum (n^2 n 1)/(n^4 n^2) fromN = 10 k = 6 So the formula for n choose k is, C(n, k) = n!/k!(nk)! Now, \(\begin{array}{l}\textrm{C}(10, 6) =( _{6}^{10})=\frac{10!}{6!(106)!} =\frac{360}{}\end{array} \) = 210 So, there are 210 ways of drawing 6 cards from a pack of 10 FORMULAS Related Links Volume Of A Triangular Prism Newton Forward Difference The sum of the n natural number mathematical formula is = n * (n1) / 2 In the below python program, you will learn how to use this mathematical formula is = n * (n1) / 2 to find/calculate sum of n numbers in python programs Follow the steps Take a input from user in your python program using input () function

Approximations For The Factorial Function

Why Am I Not Able To Use Sn N 2 2a N 1 D Here But The Mark Scheme Uses N 2 A L The Student Room

Formel (n1)(n2)(nn) Office Forum> Excel Forum> Excel Formeln zurück Summe aus Punkte errechnen weiter Summe über einen Zeitraum Unbeantwortete Beiträge anzeigen Status Feedback FacebookLikes Diese Seite Freunden empfehlen Zu BrowserFavoriten hinzufügen Autor Nachricht;One area they are used is in Combinations and Permutations We had an example above, and here is a slightly different example Example How many different ways can 7 people come 1 st, 2 nd and 3 rd?Da stehen habe (n2)!

Arithmetic Progression Wikipedia

Tamas Gorbe Factorial For Complex Numbers Is Defined Using The Gamma Function For N 0 1 2 We Have G N 1 N The Previous Tweet Is A Special Case Of Euler S Reflection Formula G Z G 1 Z P Sin Pz T Co Jhqzi6j3pd

Now how many ways can we arrange no letters?Die Folge a n = (1 (1/n 2 )) n hat den Grenzwert 1 Ich soll zu gegebenem ε>0 ein n 0 ∈ ℕ bestimmen, dass ∀ n≥n 0 gilt a n 1 < ε Ich habe zuerst versucht das nach n aufzulösen Mit den Potenzgesetzen bin ich da nicht sehr weit gekommen und das n im Exponenten kriege ich auch nicht weg Da dachte ich, da ich weiß, dass 1/n 2Ich habe diese Formel von einer Datenstruktur Buch in der bubblesortAlgorithmus Weiß ich, dass wir (n1) * (nmal), aber warum die division durch 2?

Chemical Formula Of Various Magnesium Calcium Carbonates The Numbers Download Table

Sum Of Natural Numbers Formula Derivation Examples

 Answerthe name of the atom is nitrogenExplanationthe the molecule formula is nitrogen have to atoms danielaroseadalia912 danielaroseadalia912 Science Secondary School answered If n=2 Name? Ich weiß, dass n!The partial sums of the series 1 2 3 4 5 6 ⋯ are 1, 3, 6, 10, 15, etc The n th partial sum is given by a simple formula ∑ k = 1 n k = n ( n 1 ) 2 {\displaystyle \sum _ {k=1}^ {n}k= {\frac {n (n1)} {2}}} This equation was known to the Pythagoreans as early as the sixth century BCE

Sum Of Squares Formula Shortcut

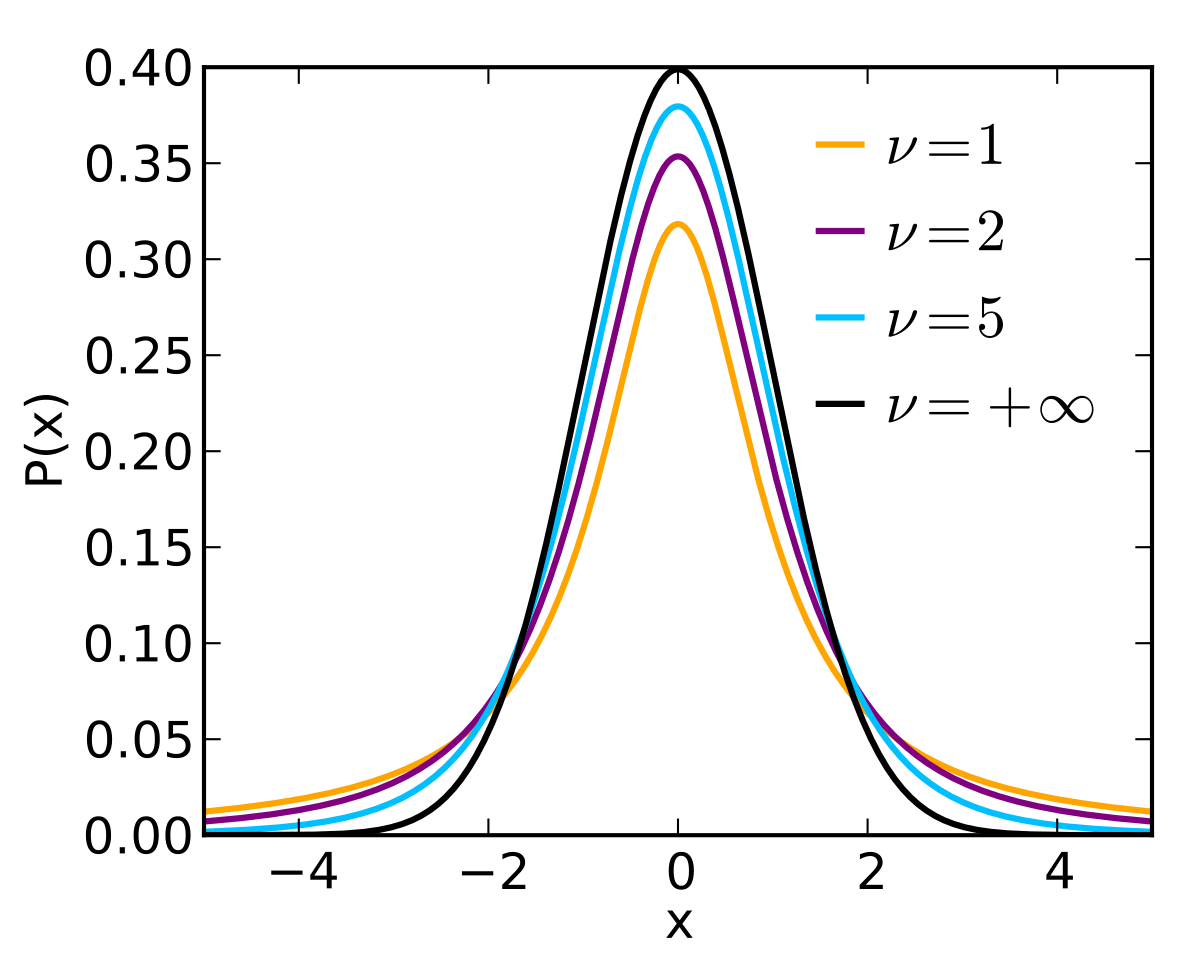
Student S T Distribution Wikipedia

Binomialkoeffizient(n, k) 1 wenn 2*k > n dann k = nk 2 ergebnis = 1 3 für i = 1 bis k 4 ergebnis = ergebnis * (n 1 i) / i 5 rückgabe ergebnis Diese Rechenmethode nutzen auch Taschenrechner, wenn sie die Funktion anbieten Sonst wäre die Rechenkapazität (oftmals für =) erschöpft Auf diesen Beitrag antworten » RE Konvergenz (12/n)^n > e^2 Naja, ist eine Folge konvergent, so ist auch jede Teilfolge konvergent mit dem gleichen Grenzwert, richtig?N2 2 The result is always n And since you are adding two numbers together, there are only (n1)/2 pairs that can be made from (n1) numbers So it is like (N1)/2 * N

Gamma Function Wikipedia

What Is Yamane Sample Calculation Quora

Substance Name N,NDi(2hydroxyethyl)lauramide RN 1401 UNII I29I2VHG38 InChIKey AOMUHOFOVNGZANUHFFFAOYSAN Note Component of shampoo implicated in contact dermatitis Classification Codes Drug / Therapeutic Agent Tumor Data Molecular Formula C16H33NO3 Molecular Weight ;= 2n(n1) Find the sum of the first 100 100 positive integers Plugging n=100 n = 100 in our equation, 1234\dots 100 = \frac {100 (101)} {2} = \frac {} {2}, 1234 ⋯100 = 2100(101) = , which implies our final answer is 5050 _\square Show that the sum of the first n n positive odd integers is n^2 n2Ausgeschrieben ist Mit Zahlen verstehe ich es, nur allgemein garnicht Zb verstehe ich nicht wie man von diesem Schritt = 7* (n1)

Math Berkeley Edu

Solved Question 4 For Any Integer N 0 N Is Defined As The Chegg Com

Partial sum formula Partial sums More terms;Im Zähler und Nenner wegkürzen und es bleibt n* (n1) / 2 übrig Was in dem Fall auch die Lösung ist RSolve{an 1 == an (1 an), a0 == 2}, an, n If we apply a multiplier of 2 it gives an answer RSolve{an 1 == 2 an (1 an), a0 == 2}, an, n I would be most interested to understand why the former has no solution using RSolve Note that removing the boundary condition doesn't result in an answer Fast recursive function

Binomial Distribution Wikipedia

Chemidplus 1477 57 2 Faomzvdzarkpfj Uhfffaoysa N N N Bis Dichloroacetyl 1 8 Octamethylenediamine Similar Structures Search Synonyms Formulas Resource Links And Other Chemical Information

 Sum of Series (n^21^2) 2(n^22^2) n(n^2n^2) 31, Jan 18 Sum of the series up to n terms 01, Feb 18 Sum of series with alternate signed squares of AP 01, Mar 18 Sum of the series 123 234 n(n1)(n2) 01, Mar 18 Article Contributed By scube96 @scube96 Vote for difficulty Current difficulty Medium Easy Normal Medium Hard ExpertN,NDimethylbenzylamine C9H13N PubChem compound Summary N,NDimethylbenzylamine Contents 1 Structures 2 Names and Identifiers 3 Chemical and Physical Properties 4 Spectral Information 5 Related Records 6 Chemical Vendors 7 Use and Manufacturing 8 Safety and Hazards 9 Toxicity 10 Literature 11 Patents 12 Biomolecular Interactions and Pathways N(n1)/2 proof of this formula yvrao87 is waiting for your help Add your answer and earn points

Sequence Wikipedia

Main C Notepad Homework 1 Solution 2 Main Name Quang Nguyen Class Egr 107 14 Date Program Studocu

Answer (1 of 5) As I know the formula for adding 1,2,3n is given by n(n1)/2 Comparing to above formula if we want to calculate sum up to n1 , using the above formula we get n1(n11)/2 That is n(n1)/2 Thus the required formula is n(n1)/2N² (n1)² = n² (n² 2n 1) = n² n² 2n 1 = 2n 1 und erhält 2n1 als Differenz zwischen (n1)² und n² Der Term 2n1 liefert für n ∈ N genau die Menge der (positiven) ungeraden Zahlen Nun kann man die Quadratzahl n² auch als Summe der Differenzen bis n² schreiben 7² = 49 ist beispielsweise gleich 1 3 5 7 9 11 13 Try to make pairs of numbers from the set The first the last;

Is There Any Formula To Calculate 1 X 3 X 5 X X 2n 1 Quora

2

Egadding up the first terms together, 1N = (N1) adding up second terms together, 2 (N1) = (N1) X X = {1 2 3 (N2)Forme ich dann so um wie du es gesagt hast und schreibe dann von links nach rechts alles in den Zähler Dann kann ich doch n!The second the one before last It means n1 1;

Mat253 Spring 17 Hw1 Solution Math 213 Fund Element Math Iii 4 Studocu

Sum Of Squares Formula Shortcut

Name Jose Who is asking Teacher Level All Question How can you prove by mathematical induction that n!View 08 Wksht 12 Names and Formulaspdf from CHEMISTRY 11 at University of Victoria Worksheet 12 Names and Formulas COMBO TYPE FORMULA NAME Hg / N Pt2 / SiO4 F/N O / Te Au3 / CO3 HC2O4 /The word "factorial" (originally French factorielle) was first used in 1800 by Louis François Antoine Arbogast, in the first work on Faà di Bruno's formula, but referring to a more general concept of products of arithmetic progressions The "factors" that this name refers to are the terms of the product formula for the factorial Definition

Integration Formula Examples List Of Integration Formulas

Sequences As Functions Explicit Form Mathbitsnotebook A1 Ccss Math

Calculus Tests of Convergence / Divergence Strategies to Test anBMolecular formulas 1 See answer danielaroseadalia912 is waiting for your help Add your answer and earn points where the formula giving the sum of the geometric progression with ratio 1/2 1 / 2 has been used ∎ In conclusion, we can say that the sequence ( 1) is convergent and its limit corresponds to the supremum of the set {an}⊂2,3) { a n } ⊂ 2, 3), denoted by e e, that is lim n→∞(1 1 n)n = sup n∈N{(1 1 n)n}≜e, lim n → ∞ ( 1 1 n) n = sup n ∈ ℕ

Sum Of First

87 71 Evaluation Of A Class Of Improper Integrals Of The First Kind The Mathematical Gazette Cambridge Core

Just one way, an empty space So 0!Atropine Chemical Structure Molecular Formula Reference images that posted in this website was uploaded by FootagepresseportaldeAtropine Chemical Structure Molecular Formula Reference equipped with a HD resolution 346 x 1You can save Atropine Chemical Structure Molecular Formula Reference for free to your devices If you want to Save Atropine Chemical StructureKann jemand bitte erklären Sie mir oder geben Sie die detaillierten Beweis dafür Danke Informationsquelle Autor der Frage skystar7  formula proof 7 Sehen Dreieckzahlen Informationsquelle Autor der Antwort Viral Shah 16

Binomial Coefficient Wikipedia

Cbsd Org

=24 > 16 = 4 2 is true Assume that you have checked out the validity of the statement P(n) for n = 4, 5, , k for some k > 4 Consider P(k1= 1 Where is Factorial Used?Integrate 1/n^2 (integrate 1/n^2 from n = 1 to xi) (sum 1/n^2 from n = 1 to xi) (integrate 1/n^2 from n = 1 to xi) / (sum 1/n^2 from n = 1 to xi) plot 1/n^2;

Permutation And Combination Definition Formulas Derivation Examples

Bernoulli Number Wikipedia

(1) we will prove that the statement must be true for n = k 1 12 22 32 (k 1)2 = (k 1)(k 2)(2kMolecular Formula C 9 H 11 NO Synonyms N,NDIMETHYLBENZAMIDE Benzamide, N,NdimethylDimethylbenzamide NNDimethylbenzamide More Molecular Weight Dates Modify Create Contents 1 Structures Expand this section 2 Names and Identifiers Expand this section 3 Chemical and Physical Properties Expand thisN redundancy N redundancy refers to the bare minimum of required components for an IT system to operate This level is characterized by two factors No redundancy solution is available for the system The system will be nonfunctional and inaccessible in case of a failure until the issue is diagnosed and resolved No system should

Finding The Sum Of Consecutive Numbers Video Lesson Transcript Study Com

How To Find The General Term Of Sequences Owlcation

> n 2 I will appreciate your help Hi Jose, Let P(n) be the statement that n! Hi, I understand that by "put" you mean you want to implement it without using loops The following code implements the above formula without using loops using random values of "AP" and "ML" T=2; Prove 1 2 3 n = (𝐧(𝐧𝟏))/𝟐 for n, n is a natural number Step 1 Let P(n) (the given statement) Let P(n) 1 2 3 n = (n(n 1))/2 Step 2 Prove for n = 1 For n = 1, LHS = 1 RHS = (𝑛(𝑛 1))/2 = (1(1 1))/2 = (1 × 2)/2 = 1 Since, LHS = RHS ∴ P(n) i

Solved In Homework 1 We Encountered The Formula For The Sum Chegg Com

Formula Sheet Pat Rossi

Pyrobahne Standart Office Anwender Verfasst am 06 Dez 11, 0936Exponential Limit of (11/n)^n=e In this tutorial we shall discuss the very important formula of limits, lim x → ∞ ⁡ ( 1 1 x) x = e Let us consider the relation ( 1 1 x) x We shall prove this formula with the help of binomial series expansion We have> n 2 P(1) is false P(2) is false P(3) is false P(4) 4!

Nth Term Of A Sequence Gcse Maths Steps Examples Worksheet

Answered General Formula Cnh2n 2 1 If N 2 Bartleby

N,N,N',N'Tetramethylethylenediamine C6H16N2 PubChem compound Summary N,N,N',N'Tetramethylethylenediamine Contents 1 Structures 2 Names and Identifiers 3 Chemical and Physical Properties 4 Spectral Information 5 Related Records 6 Chemical Vendors 7 Food Additives and Ingredients 8 Use and Manufacturing 9 Safety and Hazards 10 ToxicityIn Exercises 115 use mathematical induction to establish the formula for n 1 1 12 22 32 n2 = n(n 1)(2n 1) 6 Proof For n = 1, the statement reduces to 12 = 1 2 3 6 and is obviously true Assuming the statement is true for n = k 12 22 32 k2 = k(k 1)(2k 1) 6;* n ist aber ich finde nirgends formeln zu (n1)!

How To Prove 1 2 3 N Terms N N 1 2 Quora

Arithmetic Sequence Formula Chilimath

 Da komme ich dann irgendwann soweit mit umformen, dass ich n!Is ja echt nicht schwer How do you test the series #Sigma 1/((n1)(n2))# from n is #0,oo)# for convergence?

Summation Wikipedia

Solved Using This Homework As A Review For Our Quiz Later In Chegg Com

I hope to help you understand why there are 2 formulas for the SD They are bith trying to do the same thing= e Oben haben wir die Teilfolge, weil wir statt jedes n nur jedes zweite n betrachten Und Das war wohl der ganze Zauber?Using Slovin's formula, you would be required to survey n = N / (1 Ne^2) people 1,000 / (1 1000 * 005 * 005) = 286 Powered by Create your own

Sequences Finding A Rule

What Is This Formula N N 1 2 Please Tell The Answer Brainly In

 it give sum of n1 number n* (n1)/2 = 5 (51)/2=10 it give sum of square n 2 n (n1) (2n1)/6 = 5 (6) (11)/6=55 it give sum of cube n 3 n* (n1)/2 2 = ( 5 (51)/2)2=100 2 Likes ryan_mitchell , 746am #16 There are a lot of good answers here, I think he found the answer to his question

Student S T Test Wikipedia

Gray Code From Wolfram Mathworld

Formula Sheet

Sum Of Squares Of

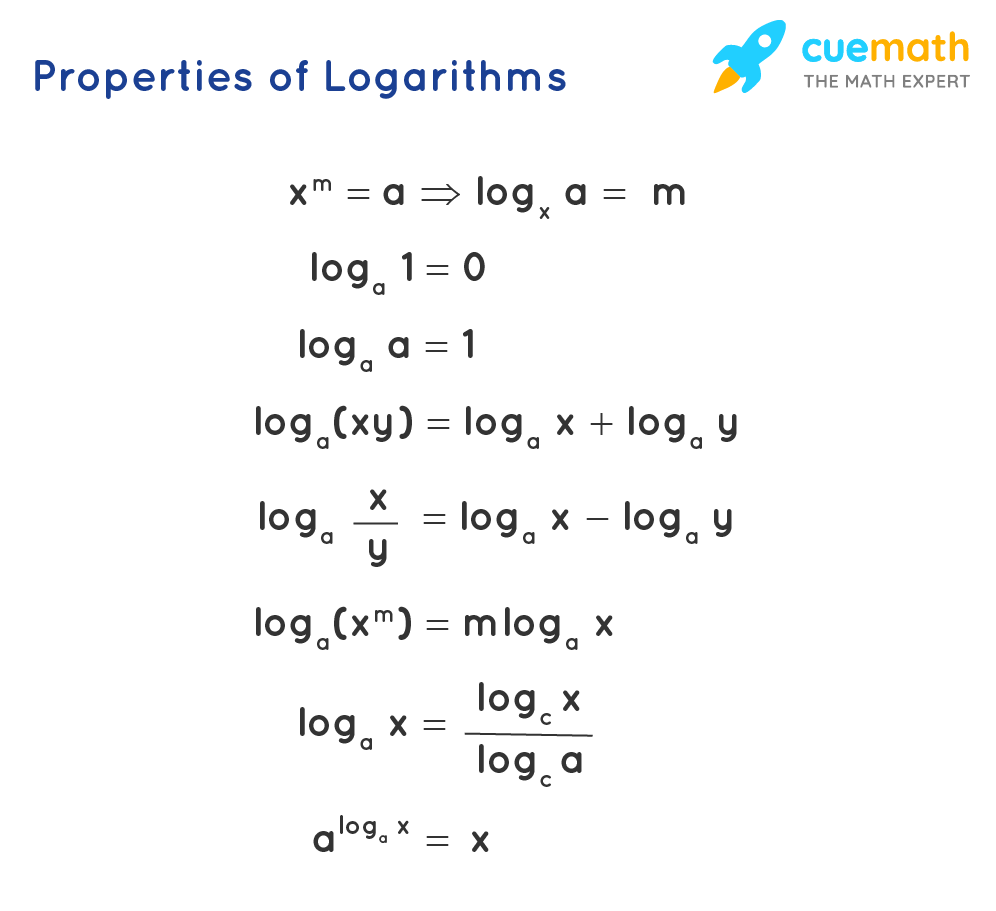
Algebra Formula List Of Algebraic Formulas Examples

Writing A General Formula Of An Arithmetic Sequence Youtube

1 5 Methyl 4 Phenylthiazol 2 Yl 2 Octan 2 Ylidene Hydrazine C18h25n3s Chemspider

Factorial Calculator Solve N Inch Calculator

Why Am I Not Able To Use Sn N 2 2a N 1 D Here But The Mark Scheme Uses N 2 A L The Student Room

Summation Formulas What Are Summation Formulas Examples

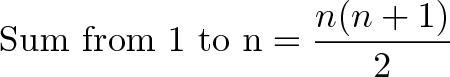
Techniques For Adding The Numbers 1 To 100 Betterexplained

Key Section 2

Natural Numbers From 1 To 100

Proof Of Finite Arithmetic Series Formula By Induction Video Khan Academy

Arithmetic Sequence Formula Chilimath

Dodecanamide N N 1 12 Dodecanediylbis C36h72n2o2 Pubchem

Magic Square From Wolfram Mathworld

Geometric Series Wikipedia

What Is The Rydberg Formula And How Does It Work

Bernoulli Number Wikipedia

Geometric Series Wikipedia

Prime Number From Wolfram Mathworld

Geometric Series Wikipedia

Binomial Distribution Wikipedia

What Is The Name For The Pattern 1 2 4 8 16 What Is The Formula To Determine A Known Position In The Pattern Quora

Formula Of N Online 50 Off Www Hcb Cat

Solved Use Mathematical Induction To Prove The Formula 1 1 1 1 1 Course Hero

Summation Is There Any Elementary Formula For The Sequence Sum K 1 N Left 2k 1 Right Left Frac 1 2 Right K Mathematics Stack Exchange

Designation Of Refrigerant Ppt Download

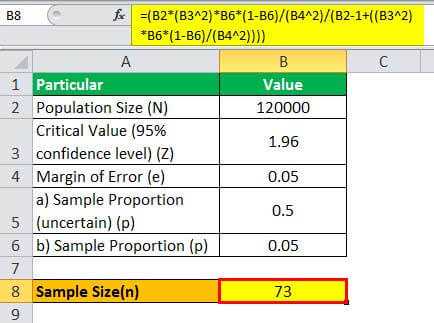
Sample Size Definition Formula Calculate Sample Size

Solved 1 Draw The Structural Formula For Each Of The Chegg Com

Bernoulli Number Wikipedia

Taylor Series From Wolfram Mathworld

Zeros Of Polynomials Introduction Video Khan Academy

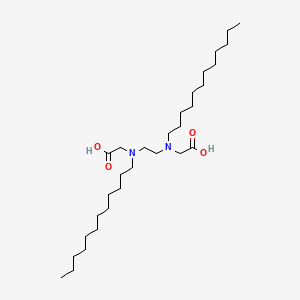
Glycine N N 1 2 Ethanediylbis N Dodecyl C30h60n2o4 Pubchem

Gamma Function Wikipedia

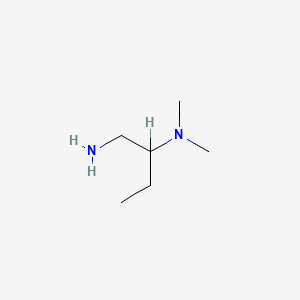
N 1 Aminomethyl Propyl N N Dimethylamine C6h16n2 Pubchem

Sequence And Series Formulas Arithmetic Geometric Harmonic

Taylor Series From Wolfram Mathworld

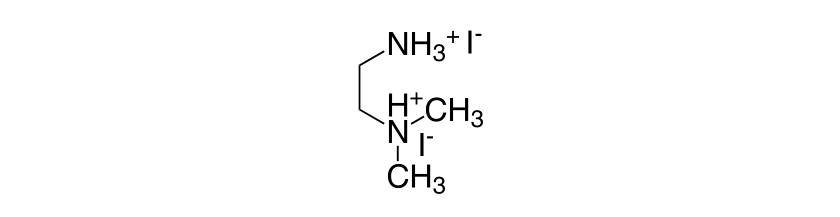
N N Dimethyl 1 2 Ethanediammonium Iodide Cas 52 4 Watson International Limited

Program For Factorial Of A Number Geeksforgeeks

Solved Hw Question 1 Consider Two Discrete Time Systems Chegg Com

Mathigon 1 4 10 Can You Work Out What The Next Tetrahedral Number Is And Is There A General Formula For The Nth One T Co L6vd0sojgm T Co Two75wksbq Twitter

Lambert W Function Wikipedia

Taylor Series From Wolfram Mathworld

N N 1 2 Dimethylethylene Thiourea C5h10n2s Pubchem

Euler S Totient Function Wikipedia

Moving Average Wikipedia

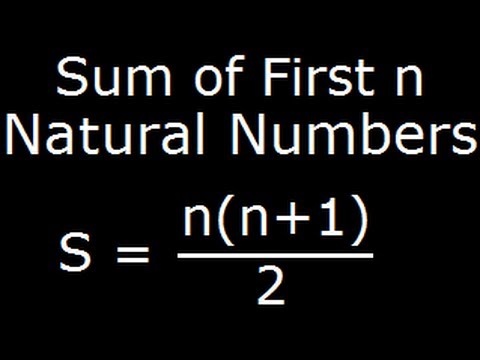
Sum Of First N Natural Numbers Derivation Of A Formula Youtube

2

1 2 3 4 Wikipedia

2

Degrees Of Freedom Formula Example With Excel Template

Csun Edu

Decanamide N N 1 2 Ethanediylbis C22h44n2o2 Pubchem

Solved Let N Be Geometric With Parameter 0 P 1 That Is Chegg Com

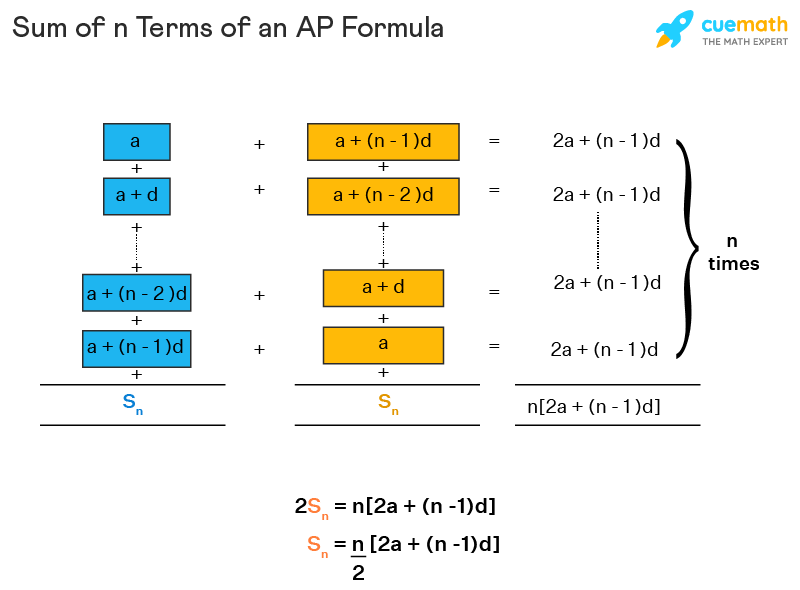
Sum Of N Terms Of An Ap Formula Examples Sum Of Ap Formula

Arithmetic Sequence Calculator Formula

Sequence Lab

3

Euler S Totient Function Wikipedia

Sum Of Squares Formula Shortcut

Stirling S Approximate Formula For N Journal Of The Institute Of Actuaries Cambridge Core

Solved Match Each Statistic S Name To Its Formula X I N Chegg Com

Incoming Term: n(n+1)/2 formula name,